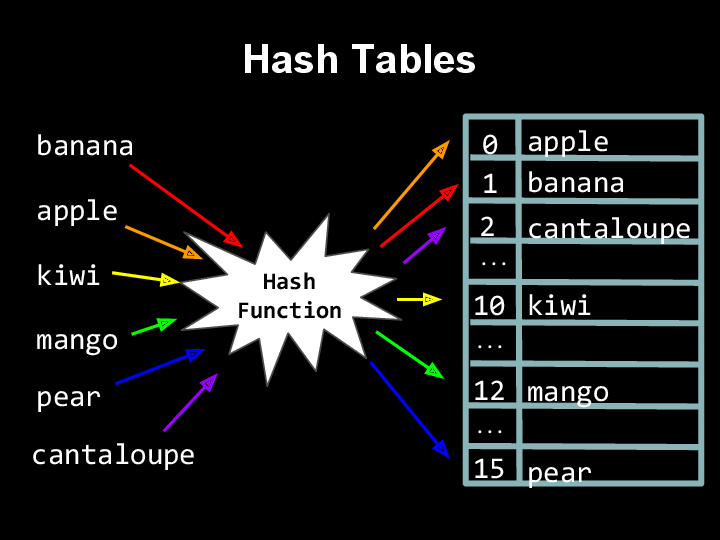
10.2.1. Hash Function Principles¶

1. Number Of Slots In Hash Tables
2. Number Of Slots In Hash Table Search

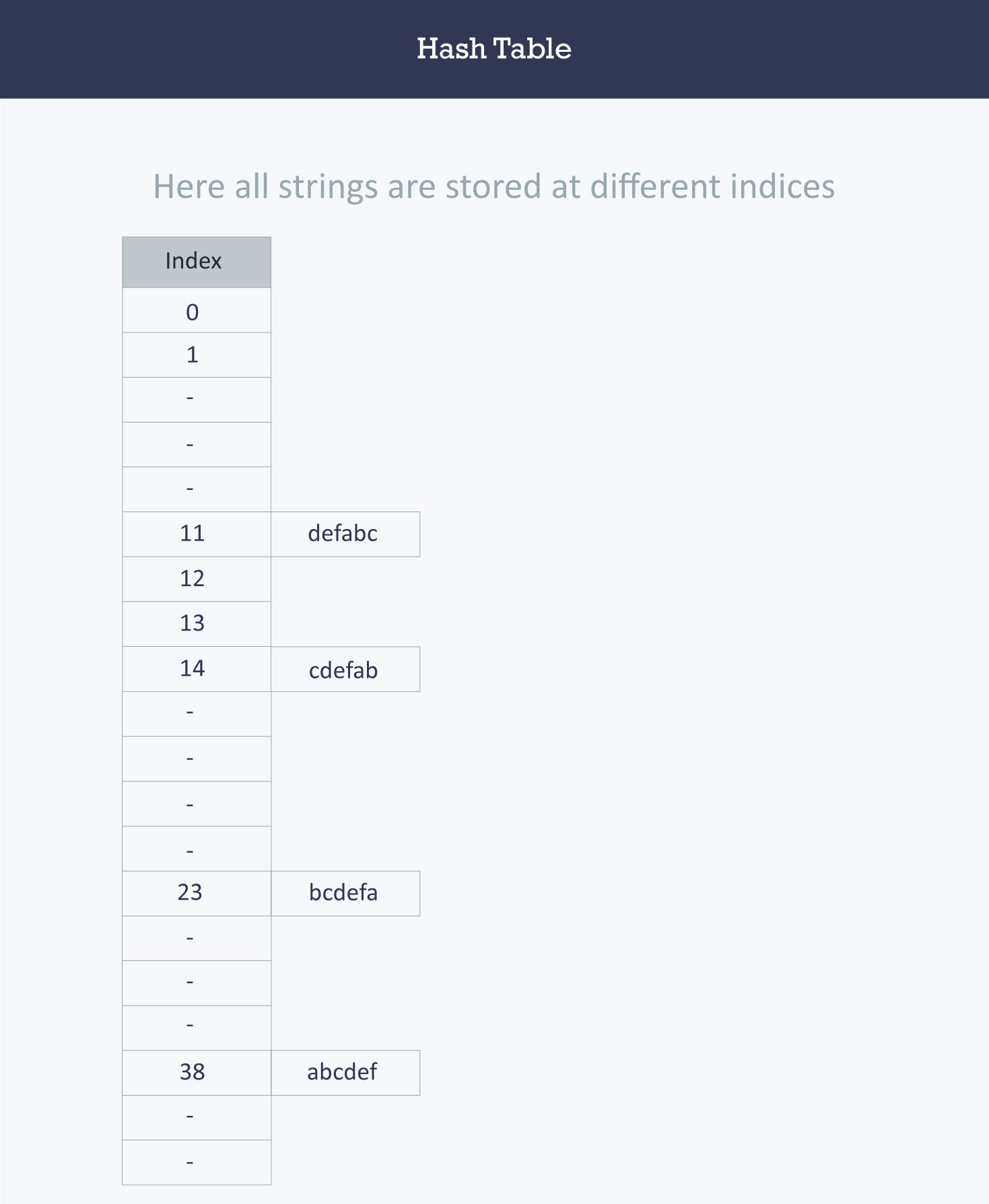
Each position of the hash table, slots, can hold an item and is named by an integer value starting at 0. We can use an Array to implement a hash table and initially all the elements of the array would be None. For Example: Insert 1, 3,5, 7, 8, 10, 11 in a hash table using hashing. Create an array arbitrary size.

Number Of Slots In Hash Tables

Hashing generally takes records whose key values come from alarge range and stores those records in a tablewith a relatively small number of slots.Collisions occur when two records hash to the same slot in thetable.If we are careful—or lucky—when selecting a hash function,then the actual number of collisions will be few.Unfortunately, even under the best of circumstances, collisions arenearly unavoidable.To illustrate, consider a classroom full of students.What is the probability that some pair of studentsshares the same birthday (i.e., the same day of the year, notnecessarily the same year)?If there are 23 students, then the odds are about even that two willshare a birthday.This is despite the fact that there are 365 days in which studentscan have birthdays (ignoring leap years).On most days, no student in the class has a birthday.With more students, the probability of a shared birthday increases.The mapping of students to days based on their birthday is similar toassigning records to slots in a table (of size 365) using thebirthday as a hash function.Note that this observation tells us nothing about whichstudents share a birthday, or on which days of the year sharedbirthdays fall.

Try it for yourself.You can use the calculator to see the probability of a collision.The default values are set to show the number of people in a room suchthat the chance of a duplicate is just over 50%.But you can set any table size and any number of records to determinethe probability of a collision under those conditions.

1. Say we are given keys in the range 0 to 999, and have a hash table of size 10. In this case, a possible hash function might simply divide the key value by 100. Thus, all keys in the range 0 to 99 would hash to slot 0, keys 100 to 199 would hash to slot 1, and so on.
2. Hash Tables with Chaining. A simple resolution: Put elements that hash to the same slot into a linked list. This is called chaining because we chain elements off the slot of the hash table. Slot j points to the head of a list of all stored elements that hash to j, or to NIL if there are no such elements.

Use the calculator to answer the following questions.

To be practical, a database organized by hashing must store records in ahash table that is not so large that it wastes space.To balance time and space efficiency, this means that the hash tableshould be around half full.Because collisions are extremely likely to occur under these conditions(by chance, any record inserted into a table that is half full shouldhave a collision half of the time),does this mean that we need not worry about how well a hash functiondoes at avoiding collisions?Absolutely not.The difference between using a good hash function and a bad hash functionmakes a big difference in practice in the number of records that must beexamined when searching or inserting to the table.Technically, any function that maps all possible key values to aslot in the hash table is a hash function.In the extreme case, even a function that maps all records to the sameslot in the array is a hash function, but it does nothing to help usfind records during a search operation.

Number Of Slots In Hash Table Search

We would like to pick a hash function that maps keysto slots in a way that makes each slot in the hash table have equalprobablility of being filled for the actual set keys being used.Unfortunately, we normally have no control over the distribution ofkey values for the actual records in a given database or collection.So how well any particular hash function doesdepends on the actual distribution of the keys used within theallowable key range.In some cases, incoming data are well distributed across their keyrange.For example, if the input is a set of random numbers selecteduniformly from the key range,any hash function that assigns the key range so that each slot in thehash table receives an equal share of the range will likely alsodistribute the input records uniformly within the table.However, in many applications the incoming records are highlyclustered or otherwise poorly distributed.When input records are not well distributed throughout the key rangeit can be difficult to devise a hash function that does a good job ofdistributing the records throughout the table, especially if theinput distribution is not known in advance.

There are many reasons why data values might be poorly distributed.

1. Natural frequency distributions tend to follow a common pattern wherea few of the entities occur frequently while most entities occurrelatively rarely.For example, consider the populations of the 100 largest cities inthe United States.If you plot these populations on a numberline, most of themwill be clustered toward the low side, with a fewoutliers on the high side.This is an example of a Zipf distribution.Viewed the other way, the home town for a given person is far morelikely to be a particular large city than a particular small town.
2. Collected data are likely to be skewed in some way.Field samples might be rounded to, say, thenearest 5 (i.e., all numbers end in 5 or 0).
3. If the input is a collection of common English words, the beginningletter will be poorly distributed.

Note that for items 2 and 3 on this list,either high- or low-order bits of the key are poorly distributed.

When designing hash functions, we are generally faced with one of twosituations:

1. We know nothing about the distribution of the incoming keys.In this case, we wish to select a hash function that evenlydistributes the key range across the hash table,while avoiding obvious opportunities for clustering such as hashfunctions that are sensitive to the high- or low-order bits of the keyvalue.
2. We know something about the distribution of the incoming keys.In this case, we should use a distribution-dependent hash functionthat avoids assigning clusters of related key values to the same hashtable slot.For example, if hashing English words, we should not hash onthe value of the first character because this is likely to be unevenlydistributed.

In the next module, you will see several examples of hash functionsthat illustrate these points.